What do the two have in common ? It seems that the two notions come from completely different worlds - one from Astrophysics, concerning galaxy clusters tens of Megaparsecs in size, and the other from the humble scale of the families, a few meters in size. Thats 23 orders of magnitudes of difference !

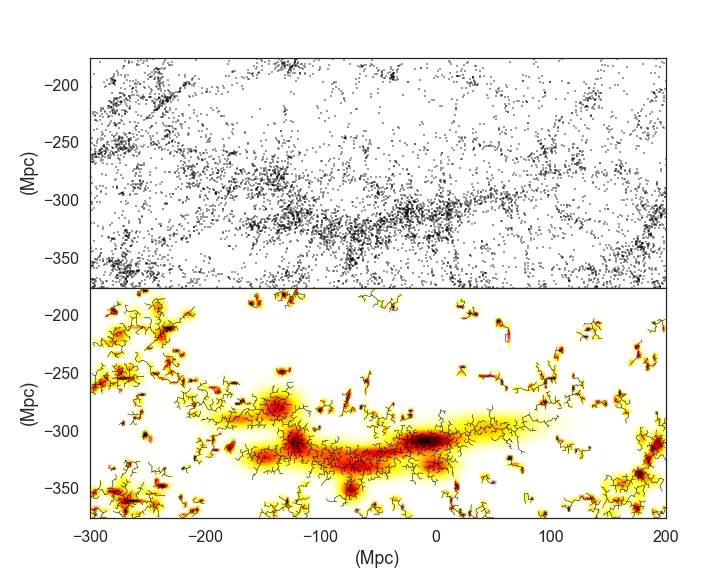
Fig.1 shows what galaxies look like when viewed from a great distance of redshift z=0.780 (few thousands of Megaparsecs ). Each dot in this image is an individual galaxy, containing each on average a billion of stars.

Galaxy Clustering
Fig.1 : This figure shows on the upper panel galaxies forming a giant structure so-called SDSS Great Wall. The lower panel shows clustering based on a minimum spanning tree dendrogram, which connects the closest neighbors into a cluster - only clusters with 30 galaxies or more are shown. The figure is based on the data presented in Figure 1 of Cowan & Ivezic (2008). I modified the code, based on the publicly available SDSS dataset. A similar figure appears in the book “Statistics, Data Mining, and Machine Learning in Astronomy”, by Ivezic, Connolly, Vanderplas, and Gray (2013).

In our project we are interested in family homelessness , and therefore we need to identify families, but families are not a fixed notion in our data. Indeed, we found that some persons appear in different families, and this leads to the necessity of finding families in the dataset not necessarily by sharing a family identification number. In clustering algorithms groups are found by looking for pairs of points that are closest together in a given metric. Therefore, to apply a clustering algorithm to our data, we need to define a metric. In our case we postulate that the inverse of the frequency of sharing the same family identification number is a good definition of a distance. According to that metric, persons which appear frequently with the same family identification number are closer in that abstract space.

Here is where the advantage of using clustering algorithms comes to hand. In case of galaxies, we are looking at their physical positions in space, and we can ‘by eye’ find those clusters: a computer algorithm can only help make this task quicker and more quantifiable. However, in case of searching for families, we are creating an abstract space, where clustering algorithms allow us to find patterns that otherwise would be completely obscured.

Hierarchical clustering in particular partitions the data into as many clusters as there are points in the dataset (eg. N) . Then at each iteration, the clusters are merged, so that we have one less : N-1 clusters. This is repeated until at the last, N-th merger, there is only one cluster that contains all data. In hierarchical clustering the two points that remain together in one cluster also belong to one cluster at all subsequent iterations. At any point, relations between points can be visualised with a tree diagram (see Fig. 1) . The method of Hierarchical Clustering can be also very well understood on this example , which considers a grid of distances between US cities.

In conclusion, we can see that vastly different scales can be united by an algorithmically similar approach, and therefore galaxy clustering is connected to searching for families in a dataset. I am excited that a method that was developed for abstract purposes can be applied towards social good.